API¶

Limbo follows a policy-based design, which allows users to combine high flexibility (almost every part of Limbo can be substituted by a user-defined part) with high performance (the abstraction do not add any overhead, contrary to classic OOP design). These two features are critical for researchers who want to experiment new ideas in Bayesian optimization. This means that changing a part of limbo (e.g. changing the kernel functions) usually corresponds to changing a template parameter of the optimizer.

The parameters of the algorithms (e.g. an epsilon) are given by a template class (usually called Params in our code, and always the first argument). See Parameters for details.

To avoid defining each component of an optimizer manually, Limbo provides sensible defaults. In addition, Limbo relies on Boost.Parameter to make it easy to customize a single part. This Boost library allows us to write classes that accept template argument (user-defined custom classes) by name. For instance, to customize the stopping criteria:

using namespace limbo;

// here stop_t is a user-defined list of stopping criteria
bayes_opt::BOptimizer<Params, stopcrit<stop_t>> boptimizer;

Or to define a custom acquisition function:

using namespace limbo;

// here acqui_t is a user-defined acquisition function
bayes_opt::BOptimizer<Params, acquifun<acqui_t>> boptimizer;

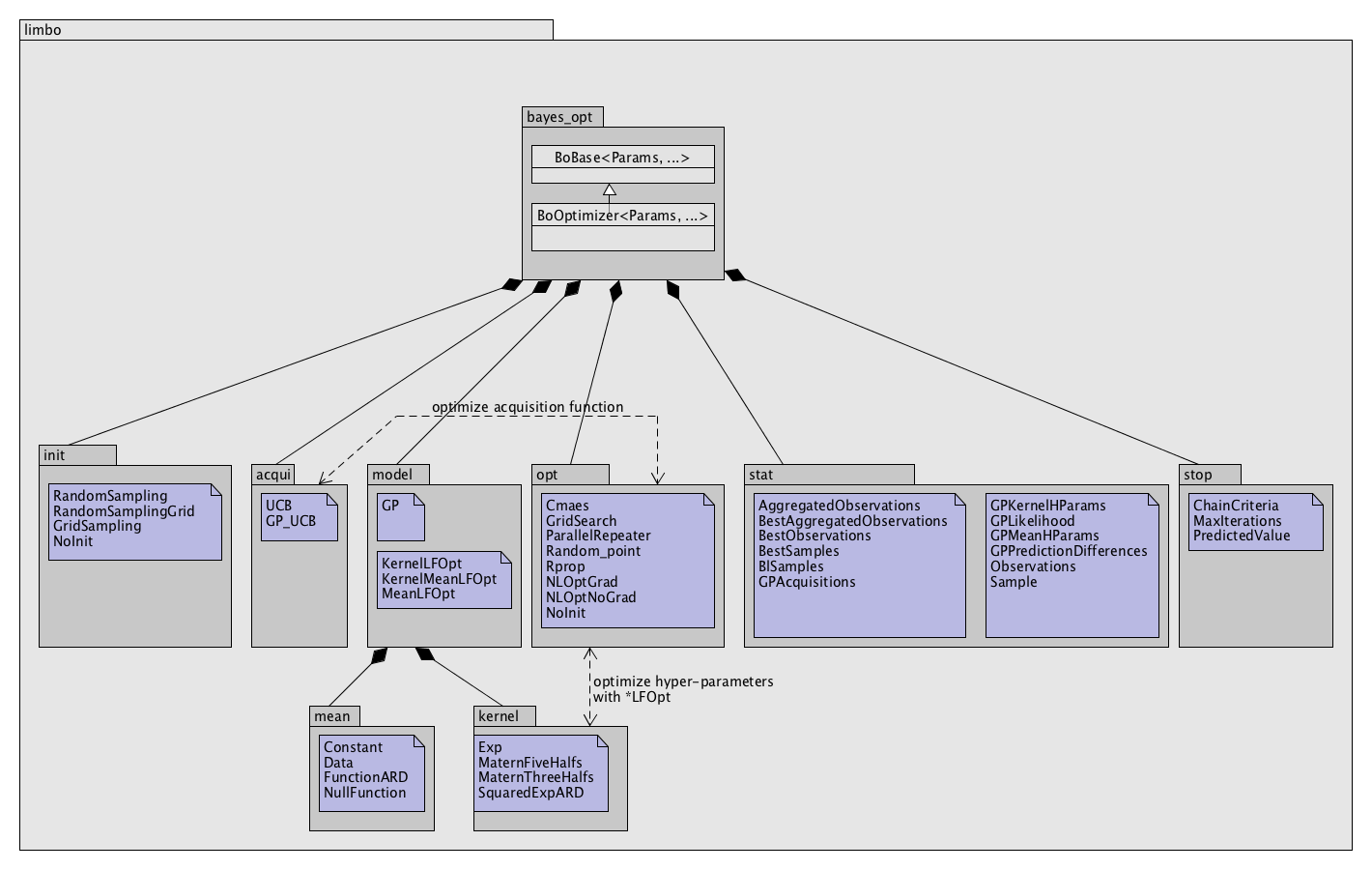
Class Structure¶

Click on the image to see it bigger.

There is almost no explicit inheritance in Limbo because polymorphism is not used. However, each kind of class follow a similar template (or ‘concept’), that is, they have to implement the same methods. For instance, every initialization function must implement a operator() method:

template <typename StateFunction, typename AggregatorFunction, typename Opt>
void operator()(const StateFunction& seval, const AggregatorFunction&, Opt& opt) const

However, there is no need to inherit from a particular ‘abstract’ class.

Every class is parametrized by a Params class that contains all the parameters.

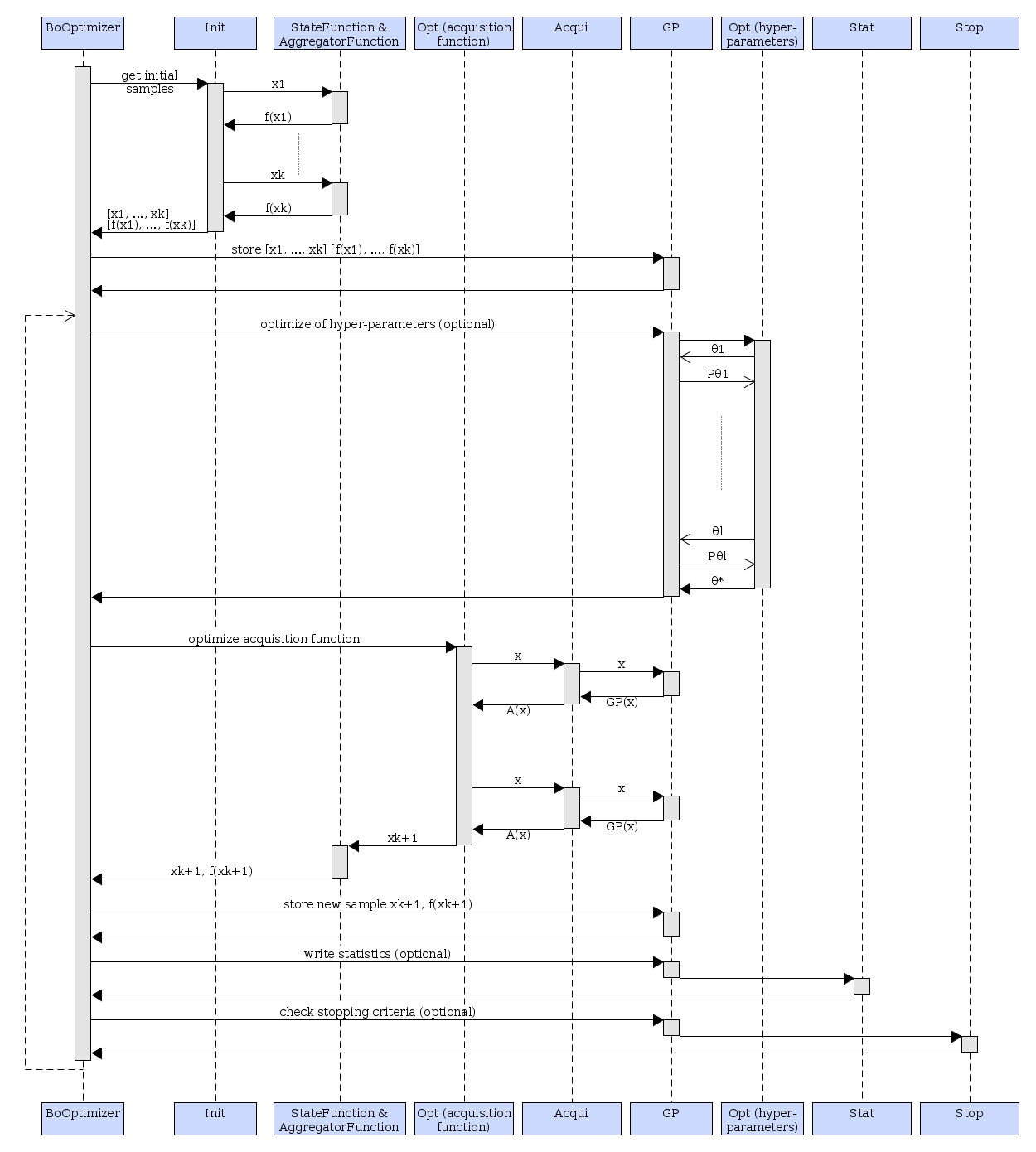
Sequence diagram¶

Click on the image to see it bigger.

File Structure¶

(see below for a short explanation of the concepts)

src
+-- limbo:
     |-- acqui: acquisition functions
     |-- bayes_opt: bayesian optimizers
     |-- init: initialization functions
     |-- kernel: kernel functions
     |-- mean: mean functions
     |-- model: models (Gaussian Processes)
     |-- opt: optimizers (Rprop, CMA-ES, etc.)
     |-- stat: statistics (to dump data)
     |-- stop: stopping criteria
     |-- tools: useful macros & small functions
|-- tests: unit tests
|-- benchmarks: a few benchmark functions
|-- examples: a few examples
|-- cmaes: [external] the CMA-ES library,
    used for inner optimizations -- from https://www.lri.fr/~hansen/cmaesintro.html
|-- ehvi: [external] the Expected HyperVolume Improvement,
    used for Multi-Objective Optimization -- by Iris Hupkens

Each directory in the limbo directory corresponds to a namespace with the same name. There is also a file for each directory called “directory.hpp” (e.g. acqui.hpp) that includes the whole namespace.

Bayesian optimizers (bayes_opt)¶

template <class Params, class A1 = boost::parameter::void_, class A2 = boost::parameter::void_, class A3 = boost::parameter::void_, class A4 = boost::parameter::void_, class A5 = boost::parameter::void_, class A6 = boost::parameter::void_>

class limbo::bayes_opt::BoBase¶

Base class for Bayesian optimizers

Parameters:

bool Params::bayes_opt_bobase::stats_enabled: activate / deactivate the statistics

This class is templated by several types with default values (thanks to boost::parameters).

type	typedef	argument	default
init. func.	init_t	initfun	RandomSampling
model	model_t	modelfun	GP<…>
acquisition fun.	aqui_t	acquifun	GP_UCB
statistics	stat_t	statfun	see below
stopping crit.	stop_t	stopcrit	MaxIterations

For GP, the default value is: model::GP<Params, kf_t, mean_t, opt_t>>,

with kf_t = kernel::SquaredExpARD<Params>
with mean_t = mean::Data<Params>
with opt_t = model::gp::KernelLFOpt<Params>

(meaning: kernel with automatic relevance determination and mean equals to the mean of the input data, that is, center the data automatically)

For Statistics, the default value is: boost::fusion::vector<stat::Samples<Params>, stat::AggregatedObservations<Params>, stat::ConsoleSummary<Params>>

Example of customization:

using Kernel_t = kernel::MaternFiveHalves<Params>;
using Mean_t = mean::Data<Params>;
using GP_t = model::GP<Params, Kernel_t, Mean_t>;
using Acqui_t = acqui::UCB<Params, GP_t>;
bayes_opt::BOptimizer<Params, modelfun<GP_t>, acquifun<Acqui_t>> opt;

Subclassed by limbo::bayes_opt::BOptimizer< Params, A1, A2, A3, A4, A5, A6 >, limbo::experimental::bayes_opt::BoMulti< Params, A1, A2, A3, A4, A5, A6 >, limbo::experimental::bayes_opt::CBOptimizer< Params, A1, A2, A3, A4, A5, A6, A7 >

Public Functions

BoBase()¶: default constructor

BoBase(const BoBase &other)¶: copy is disabled (dangerous and useless)

BoBase &operator=(const BoBase &other)¶: copy is disabled (dangerous and useless)

bool stats_enabled() const¶: return true if the statitics are enabled (they can be disabled to avoid dumping data, e.g. for unit tests)

const std::string &res_dir() const¶: return the name of the directory in which results (statistics) are written

const std::vector<Eigen::VectorXd> &observations() const¶: return the vector of points of observations (observations can be multi-dimensional, hence the VectorXd) f(x)

const std::vector<Eigen::VectorXd> &samples() const¶: return the list of the points that have been evaluated so far (x)

int current_iteration() const¶: return the current iteration number

void add_new_sample(const Eigen::VectorXd &s, const Eigen::VectorXd &v)¶

Add a new sample / observation pair

does not update the model!
we don’t add NaN and inf observations

template <typename StateFunction>
void eval_and_add(const StateFunction &seval, const Eigen::VectorXd &sample)¶: Evaluate a sample and add the result to the ‘database’ (sample / observations vectors) it does not update the model.

template <class Params, class A1 = boost::parameter::void_, class A2 = boost::parameter::void_, class A3 = boost::parameter::void_, class A4 = boost::parameter::void_, class A5 = boost::parameter::void_, class A6 = boost::parameter::void_>

class limbo::bayes_opt::BOptimizer¶

The classic Bayesian optimization algorithm.

References: [brochu2010tutorial][Mockus2013]

This class takes the same template parameters as BoBase. It adds:

type	typedef	argument	default
acqui. optimizer	acquiopt_t	acquiopt	see below

The default value of acqui_opt_t is:

opt::NLOptNoGrad<Params, nlopt::GN_DIRECT_L_RAND> if NLOpt was found in waf configure
opt::Cmaes<Params> if libcmaes was found but NLOpt was not found
opt::GridSearch<Params> otherwise (please do not use this: the algorithm will not work as expected!)

Inherits from limbo::bayes_opt::BoBase< Params, A1, A2, A3, A4, A5, A6 >

Public Types

template<> using base_t = BoBase<Params, A1, A2, A3, A4, A5, A6>¶: link to the corresponding BoBase (useful for typedefs)

Public Functions

template <typename StateFunction, typename AggregatorFunction = FirstElem>
void optimize(const StateFunction &sfun, const AggregatorFunction &afun = AggregatorFunction(), bool reset = true)¶: The main function (run the Bayesian optimization algorithm)

template <typename AggregatorFunction = FirstElem>
const Eigen::VectorXd &best_observation(const AggregatorFunction &afun = AggregatorFunction()) const¶: return the best observation so far (i.e. max(f(x)))

template <typename AggregatorFunction = FirstElem>
const Eigen::VectorXd &best_sample(const AggregatorFunction &afun = AggregatorFunction()) const¶: return the best sample so far (i.e. the argmax(f(x)))

Acquisition functions (acqui)¶

An acquisition function is what is optimized to select the next point to try. It usually depends on the model.

Template¶

template <typename Params, typename Model>
class AcquiName {
public:
    AcquiName(const Model& model, int iteration = 0) : _model(model) {}
    size_t dim_in() const { return _model.dim_in(); }
    size_t dim_out() const { return _model.dim_out(); }
    template <typename AggregatorFunction>
    limbo::opt::eval_t operator()(const Eigen::VectorXd& v, const AggregatorFunction& afun, bool gradient) const
    {
      // code
    }
  };

Available acquisition functions¶

group acqui

template <typename Params, typename Model>

class EI¶

#include <limbo/acqui/ei.hpp>

Classic EI (Expected Improvement). See [brochu2010tutorial], p. 14

\[\begin{split}EI(x) = (\mu(x) - f(x^+) - \xi)\Phi(Z) + \sigma(x)\phi(Z),\\\text{with } Z = \frac{\mu(x)-f(x^+) - \xi}{\sigma(x)}.\end{split}\]

Parameters:

double jitter - \(\xi\)

template <typename Params, typename Model>

class GP_UCB¶

#include <limbo/acqui/gp_ucb.hpp>

GP-UCB (Upper Confidence Bound). See [brochu2010tutorial], p. 15. See also: http://arxiv.org/abs/0912.3995

\[UCB(x) = \mu(x) + \kappa \sigma(x).\]

with:

\[\kappa = \sqrt{2 \log{(\frac{n^{D/2+2}\pi^2}{3 \delta})}}\]

where \(n\) is the number of past evaluations of the objective function and \(D\) the dimensionality of the parameters (dim_in).

Parameters:

double delta (a small number in [0,1], e.g. 0.1)

template <typename Params, typename Model>

class UCB¶

#include <limbo/acqui/ucb.hpp>

Classic UCB (Upper Confidence Bound). See [brochu2010tutorial], p. 14

\[UCB(x) = \mu(x) + \alpha \sigma(x).\]

Parameters:

double alpha

Default Parameters¶

group Acqui_defaults

Functions

limbo::defaults::acqui_ei::BO_PARAM(double, jitter, 0. 0)

limbo::defaults::acqui_gpucb::BO_PARAM(double, delta, 0. 1)

limbo::defaults::acqui_ucb::BO_PARAM(double, alpha, 0. 5)

limbo::defaults::acqui_eci::BO_PARAM(double, jitter, 0. 0)

Init functions (init)¶

Initialization functions are used to inialize a Bayesian optimization algorithm with a few samples. For instance, we typically start with a dozen of random samples.

Template¶

struct InitName {
    template <typename StateFunction, typename AggregatorFunction, typename Opt>
    void operator()(const StateFunction& seval, const AggregatorFunction&, Opt& opt) const
    {
     // code
    }

Available initializers¶

group init

template <typename Params>

struct GridSampling¶

#include <limbo/init/grid_sampling.hpp>

Grid sampling.

Parameter:

int bins (number of bins)

template <typename Params>

struct LHS¶

#include <limbo/init/lhs.hpp>

Latin Hypercube sampling in [0, 1]^n (LHS)

Parameters:

int samples (total number of samples)

template <typename Params>
struct NoInit¶: #include <limbo/init/no_init.hpp>
Do nothing (dummy initializer).

template <typename Params>

struct RandomSampling¶

#include <limbo/init/random_sampling.hpp>

Pure random sampling in [0, 1]^n

Parameters:

int samples (total number of samples)

template <typename Params>

struct RandomSamplingGrid¶

#include <limbo/init/random_sampling_grid.hpp>

Grid-based random sampling: in effect, define a grid and takes random samples from this grid. The number of bins in the grid is ``bins“^number_of_dimensions

For instance, if bins = 5 and there are 3 inputs dimensions, then the grid is 5*5*5=125, and random points will all be points of this grid.

Parameters:

int samples (total number of samples)
int bins (number of bins for each dimensions)

Default Parameters¶

group init_defaults

Functions

limbo::defaults::init_gridsampling::BO_PARAM(int, bins, 5)

limbo::defaults::init_lhs::BO_PARAM(int, samples, 10)

limbo::defaults::init_randomsampling::BO_PARAM(int, samples, 10)

limbo::defaults::init_randomsamplinggrid::BO_PARAM(int, samples, 10)

limbo::defaults::init_randomsamplinggrid::BO_PARAM(int, bins, 5)

Optimization functions (opt)¶

In Limbo, optimizers are used both to optimize acquisition functions and to optimize hyper-parameters. However, this API might be helpful in other places whenever an optimization of a function is needed.

Warning

Limbo optimizers always MAXIMIZE f(x), whereas many libraries MINIMIZE f(x)

Most algorithms are wrappers to external libraries (NLOpt and CMA-ES). Only the Rprop (and a few control algorithms like ‘RandomPoint’) is implemented in Limbo. Some optimizers require the gradient, some don’t.

The tutorial Optimization sub-API describes how to use the opt:: API in your own algorithms.

The return type of the function to be optimized is eval_t, which is defined as a pair of a double (f(x)) and a vector (the gradient):

using eval_t = std::pair<double, boost::optional<Eigen::VectorXd>>;

To make it easy to work with eval_t, Limbo defines a few shortcuts:

group opt_tools

Typedefs

using limbo::opt::eval_t = typedef std::pair<double, boost::optional<Eigen::VectorXd>>: return type of the function to optimize

Functions

eval_t no_grad(double x)¶: return with opt::no_grad(your_val) if no gradient is available (to be used in functions to be optimized)

const Eigen::VectorXd &grad(const eval_t &fg)¶: get the gradient from a function evaluation (eval_t)

double fun(const eval_t &fg)¶: get the value from a function evaluation (eval_t)

template <typename F>
double eval(const F &f, const Eigen::VectorXd &x)¶: Evaluate f without gradient (to be called from the optimization algorithms that do not use the gradient)

template <typename F>
eval_t eval_grad(const F &f, const Eigen::VectorXd &x)¶: Evaluate f with gradient (to be called from the optimization algorithms that use the gradient)

Template¶

template <typename Params>
struct OptimizerName {
  template <typename F>
  Eigen::VectorXd operator()(const F& f, const Eigen::VectorXd& init, bool bounded) const
  {
    // content
  }
};

f is the function to be optimized. If the gradient is known, the function should look like this:

limbo::opt::eval_t my_function(const Eigen::VectorXd& v, bool eval_grad = false)
{
  double fx = <function_value>;
  Eigen::VectorXd gradient = <gradient>;
  return {fx, gradient};
}

It is possible to make it a bit more generic by not computing the gradient when it is not asked, that is:

limbo::opt::eval_t my_function(const Eigen::VectorXd& v, bool eval_grad = false)
{
  double fx = <function_value>;
  if (!eval_grad)
    return opt::no_grad(v);
  Eigen::VectorXd gradient = <gradient>;
  return {fx, gradient};
}

If the gradient of f is not known:

limbo::opt::eval_t my_function(const Eigen::VectorXd& v, bool eval_grad = false)
{
  double x = <function_value>(v);
  return limbo::opt::no_grad(x);
}

init is an optionnal starting point (for local optimizers); many optimizers ignore this argument (see the table below): in that case, an assert will fail.
bounded is true if the optimization is bounded in [0,1]; many optimizers do not support bounded optimization (see the table below).
eval_grad allows Limbo to avoid computing the gradient when it is not needed (i.e. when the gradient is known but we optimize using a gradient-free optimizer).

To call an optimizer (e.g. NLOptGrad):

// the type of the optimizer (here NLOpt with the LN_LBGFGS algorithm)
opt::NLOptGrad<ParamsGrad, nlopt::LD_LBFGS> lbfgs;
// we start from a random point (in 2D), and the search is not bounded
Eigen::VectorXd res_lbfgs = lbfgs(my_function, tools::random_vector(2), false);
std::cout <<"Result with LBFGS:\t" << res_lbfgs.transpose()
          << " -> " << my_function(res_lbfgs).first << std::endl;

Not all the algorithms support bounded optimization and/or initial point:

Algo.	bounded	init
CMA-ES	yes	yes
NLOptGrad	*	*
NLOptNoGrad	*	*
Rprop	no	yes
RandomPoint	yes	no

* All NLOpt’s global optimizers must have bounds. Check NLOpt’s reference to see which algorithms support initial point.

Available optimizers¶

group opt

template <typename Params>

struct Cmaes¶

#include <limbo/opt/cmaes.hpp>

Covariance Matrix Adaptation Evolution Strategy by Hansen et al. (See: https://www.lri.fr/~hansen/cmaesintro.html)

our implementation is based on libcmaes (https://github.com/beniz/libcmaes)
Support bounded and unbounded optimization
Only available if libcmaes is installed (see the compilation instructions)
Parameters :
- int variant
- int elitism
- int restarts
- double max_fun_evals
- double fun_tolerance
- double xrel_tolerance
- double fun_target
- bool fun_compute_initial
- bool handle_uncertainty
- bool verbose
- double lb (lower bounds)
- double ub (upper bounds)

template <typename Params>

struct GridSearch¶

#include <limbo/opt/grid_search.hpp>

Grid search

Parameters:

int bins

template <typename Params, nlopt::algorithm Algorithm = nlopt::LD_LBFGS>

struct NLOptGrad¶

#include <limbo/opt/nlopt_grad.hpp>

Binding to gradient-based NLOpt algorithms. See: http://ab-initio.mit.edu/wiki/index.php/NLopt_Algorithms

Algorithms:

GD_STOGO
GD_STOGO_RAND
LD_LBFGS_NOCEDAL
LD_LBFGS
LD_VAR1
LD_VAR2
LD_TNEWTON
LD_TNEWTON_RESTART
LD_TNEWTON_PRECOND
LD_TNEWTON_PRECOND_RESTART
GD_MLSL
GD_MLSL_LDS
LD_MMA
LD_AUGLAG
LD_AUGLAG_EQ
LD_SLSQP
LD_CCSAQ

Parameters :

int iterations
double fun_tolerance
double xrel_tolerance

template <typename Params, nlopt::algorithm Algorithm = nlopt::GN_DIRECT_L_RAND>

struct NLOptNoGrad¶

#include <limbo/opt/nlopt_no_grad.hpp>

Binding to gradient-free NLOpt algorithms. See: http://ab-initio.mit.edu/wiki/index.php/NLopt_Algorithms

Algorithms:

GN_DIRECT
GN_DIRECT_L, [default]
GN_DIRECT_L_RAND
GN_DIRECT_NOSCAL
GN_DIRECT_L_NOSCAL
GN_DIRECT_L_RAND_NOSCAL
GN_ORIG_DIRECT
GN_ORIG_DIRECT_L
GN_CRS2_LM
GN_MLSL
GN_MLSL_LDS
GN_ISRES
LN_COBYLA
LN_AUGLAG_EQ
LN_BOBYQA
LN_NEWUOA
LN_NEWUOA_BOUND
LN_PRAXIS
LN_NELDERMEAD
LN_SBPLX
LN_AUGLAG

Parameters:

int iterations
double fun_tolerance
double xrel_tolerance

template <typename Params, typename Optimizer>

struct ParallelRepeater¶

#include <limbo/opt/parallel_repeater.hpp>

Meta-optimizer: run the same algorithm in parallel many times from different init points and return the maximum found among all the replicates (useful for local algorithms)

Parameters:

int repeats

template <typename Params>

struct RandomPoint¶

#include <limbo/opt/random_point.hpp>

return a random point in [0, 1]
no parameters
useful for control experiments (do not use this otherwise!)

template <typename Params>

struct Rprop¶

#include <limbo/opt/rprop.hpp>

Gradient-based optimization (rprop)

partly inspired by libgp: https://github.com/mblum/libgp
reference : Blum, M., & Riedmiller, M. (2013). Optimization of Gaussian Process Hyperparameters using Rprop. In European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning.

Parameters:

int iterations

Default parameters¶

group opt_defaults

Functions

limbo::defaults::opt_cmaes::BO_PARAM(int, restarts, 1): number of restarts of CMA-ES

limbo::defaults::opt_cmaes::BO_PARAM(double, max_fun_evals, - 1): maximum number of calls to the function to be optimized

limbo::defaults::opt_cmaes::BO_PARAM(double, fun_tolerance, - 1): threshold based on the difference in value of a fixed number of trials: if bigger than 0, it enables the tolerance criteria for stopping based in the history of rewards.

limbo::defaults::opt_cmaes::BO_PARAM(double, xrel_tolerance, - 1): tolerance for convergence: stop when an optimization step (or an estimate of the optimum) changes all the parameter values by less than tol multiplied by the absolute value of the parameter value. IGNORED if negative

limbo::defaults::opt_cmaes::BO_PARAM(double, fun_target, - 1): function value target: if bigger than 0, enables the function target criteria for stopping if the performance is greater than this value.

limbo::defaults::opt_cmaes::BO_PARAM(bool, fun_compute_initial, false): computes initial objective function value: if true, it evaluates the provided starting point (if any).

BO_PARAM(int, variant, aIPOP_CMAES)¶: sets the version of cmaes to use (possible values are: CMAES_DEFAULT, IPOP_CMAES, BIPOP_CMAES, aCMAES, aIPOP_CMAES, aBIPOP_CMAES, sepCMAES, sepIPOP_CMAES, sepBIPOP_CMAES, sepaCMAES, sepaIPOP_CMAES, sepaBIPOP_CMAES, VD_CMAES, VD_IPOP_CMAES, VD_BIPOP_CMAES

limbo::defaults::opt_cmaes::BO_PARAM(int, elitism, 0): defines elitism strategy: 0 -> no elitism 1 -> elitism: reinjects the best-ever seen solution 2 -> initial elitism: reinject x0 as long as it is not improved upon 3 -> initial elitism on restart: restart if best encountered solution is not the the final solution and reinjects the best solution until the population has better fitness, in its majority

limbo::defaults::opt_cmaes::BO_PARAM(bool, handle_uncertainty, false): enables or disables uncertainty handling: https://hal.inria.fr/file/index/docid/276216/filename/TEC2008.pdf

limbo::defaults::opt_cmaes::BO_PARAM(bool, verbose, false): enables or disables verbose mode for cmaes

limbo::defaults::opt_cmaes::BO_PARAM(double, lbound, 0. 0): lower bound (in input) for cmaes

limbo::defaults::opt_cmaes::BO_PARAM(double, ubound, 1. 0): upper bound (in input) for cmaes

limbo::defaults::opt_gridsearch::BO_PARAM(int, bins, 5): number of bins for each dimension

limbo::defaults::opt_nloptgrad::BO_PARAM(int, iterations, 500): number of calls to the optimized function

limbo::defaults::opt_nloptgrad::BO_PARAM(double, fun_tolerance, - 1): tolerance for convergence: stop when an optimization step (or an estimate of the optimum) changes the objective function value by less than tol multiplied by the absolute value of the function value. IGNORED if negative

limbo::defaults::opt_nloptgrad::BO_PARAM(double, xrel_tolerance, - 1): tolerance for convergence: stop when an optimization step (or an estimate of the optimum) changes all the parameter values by less than tol multiplied by the absolute value of the parameter value. IGNORED if negative

limbo::defaults::opt_nloptnograd::BO_PARAM(int, iterations, 500): number of calls to the optimized function

limbo::defaults::opt_nloptnograd::BO_PARAM(double, fun_tolerance, - 1): tolerance for convergence: stop when an optimization step (or an estimate of the optimum) changes the objective function value by less than tol multiplied by the absolute value of the function value. IGNORED if negative

limbo::defaults::opt_nloptnograd::BO_PARAM(double, xrel_tolerance, - 1): tolerance for convergence: stop when an optimization step (or an estimate of the optimum) changes all the parameter values by less than tol multiplied by the absolute value of the parameter value. IGNORED if negative

limbo::defaults::opt_parallelrepeater::BO_PARAM(int, repeats, 10): number of replicates

limbo::defaults::opt_rprop::BO_PARAM(int, iterations, 300): number of max iterations

Models / Gaussian processes (model)¶

Currently, Limbo only includes Gaussian processes as models. More may come in the future.

template <typename Params, typename KernelFunction = kernel::MaternFiveHalves<Params>, typename MeanFunction = mean::Data<Params>, typename HyperParamsOptimizer = gp::NoLFOpt<Params>>

class limbo::model::GP¶

A classic Gaussian process. It is parametrized by:

a kernel function
a mean function
[optionnal] an optimizer for the hyper-parameters

Public Functions

GP()¶: useful because the model might be created before knowing anything about the process

GP(int dim_in, int dim_out)¶: useful because the model might be created before having samples

void compute(const std::vector<Eigen::VectorXd> &samples, const std::vector<Eigen::VectorXd> &observations, bool compute_kernel = true)¶: Compute the GP from samples and observations. This call needs to be explicit!

void optimize_hyperparams()¶: Do not forget to call this if you use hyper-prameters optimization!!

void add_sample(const Eigen::VectorXd &sample, const Eigen::VectorXd &observation)¶: add sample and update the GP. This code uses an incremental implementation of the Cholesky decomposition. It is therefore much faster than a call to compute()

std::tuple<Eigen::VectorXd, double> query(const Eigen::VectorXd &v) const¶: \rst return :math:\mu, :math:\sigma^2 (unormalized). If there is no sample, return the value according to the mean function. Using this method instead of separate calls to mu() and sigma() is more efficient because some computations are shared between mu() and sigma(). \endrst

Eigen::VectorXd mu(const Eigen::VectorXd &v) const¶: \rst return :math:\mu (unormalized). If there is no sample, return the value according to the mean function. \endrst

double sigma(const Eigen::VectorXd &v) const¶: \rst return :math:\sigma^2 (unormalized). If there is no sample, return the max :math:\sigma^2. \endrst

int dim_in() const¶: return the number of dimensions of the input

int dim_out() const¶: return the number of dimensions of the output

Eigen::VectorXd max_observation() const¶: return the maximum observation (only call this if the output of the GP is of dimension 1)

Eigen::VectorXd mean_observation() const¶: return the mean observation (only call this if the output of the GP is of dimension 1)

int nb_samples() const¶: return the number of samples used to compute the GP

void recompute(bool update_obs_mean = true, bool update_full_kernel = true)¶: recomputes the GP

double compute_log_lik()¶: compute and return the log likelihood

Eigen::VectorXd compute_kernel_grad_log_lik()¶: compute and return the gradient of the log likelihood wrt to the kernel parameters

Eigen::VectorXd compute_mean_grad_log_lik()¶: compute and return the gradient of the log likelihood wrt to the mean parameters

double get_log_lik() const¶: return the likelihood (do not compute it return last computed)

void set_log_lik(double log_lik)¶: set the log likelihood (e.g. computed from outside)

double compute_log_loo_cv()¶: compute and return the log probability of LOO CV

Eigen::VectorXd compute_kernel_grad_log_loo_cv()¶: compute and return the gradient of the log probability of LOO CV wrt to the kernel parameters

double get_log_loo_cv() const¶: return the LOO-CV log probability (do not compute it return last computed)

void set_log_loo_cv(double log_loo_cv)¶: set the LOO-CV log probability (e.g. computed from outside)

const Eigen::MatrixXd &matrixL() const¶: LLT matrix (from Cholesky decomposition)

const std::vector<Eigen::VectorXd> &samples() const¶: return the list of samples that have been tested so far

template <typename A>
void save(const std::string &directory)¶: save the parameters and the data for the GP to the archive (text or binary)

template <typename A>
void save(const A &archive)¶: save the parameters and the data for the GP to the archive (text or binary)

template <typename A>
void load(const std::string &directory, bool recompute = true)¶: load the parameters and the data for the GP from the archive (text or binary) if recompute is true, we do not read the kernel matrix but we recompute it given the data and the hyperparameters

template <typename A>
void load(const A &archive, bool recompute = true)¶: load the parameters and the data for the GP from the archive (text or binary) if recompute is true, we do not read the kernel matrix but we recompute it given the data and the hyperparameters

The hyper-parameters of the model (kernel, mean) can be optimized. The following options are possible:

group model_opt

template <typename Params, typename Optimizer = opt::ParallelRepeater<Params, opt::Rprop<Params>>>

struct HPOpt¶

#include <limbo/model/gp/hp_opt.hpp>

optimize the likelihood of the kernel only

Subclassed by limbo::model::gp::KernelLFOpt< Params, Optimizer >, limbo::model::gp::KernelLooOpt< Params, Optimizer >, limbo::model::gp::KernelMeanLFOpt< Params, Optimizer >, limbo::model::gp::MeanLFOpt< Params, Optimizer >

template <typename Params, typename Optimizer = opt::ParallelRepeater<Params, opt::Rprop<Params>>>

struct KernelLFOpt¶

#include <limbo/model/gp/kernel_lf_opt.hpp>

optimize the likelihood of the kernel only

Inherits from limbo::model::gp::HPOpt< Params, Optimizer >

template <typename Params, typename Optimizer = opt::ParallelRepeater<Params, opt::Rprop<Params>>>

struct KernelLooOpt¶

#include <limbo/model/gp/kernel_loo_opt.hpp>

optimize the likelihood of the kernel only

Inherits from limbo::model::gp::HPOpt< Params, Optimizer >

template <typename Params, typename Optimizer = opt::ParallelRepeater<Params, opt::Rprop<Params>>>

struct KernelMeanLFOpt¶

#include <limbo/model/gp/kernel_mean_lf_opt.hpp>

optimize the likelihood of both the kernel and the mean (try to align the mean function)

Inherits from limbo::model::gp::HPOpt< Params, Optimizer >

template <typename Params, typename Optimizer = opt::ParallelRepeater<Params, opt::Rprop<Params>>>

struct MeanLFOpt¶

#include <limbo/model/gp/mean_lf_opt.hpp>

optimize the likelihood of the mean only (try to align the mean function)

Inherits from limbo::model::gp::HPOpt< Params, Optimizer >

template <typename Params>
struct NoLFOpt¶: #include <limbo/model/gp/no_lf_opt.hpp>
do not optimize anything

See the Gaussian Process tutorial for a tutorial about using GP without using a Bayesian optimization algorithm.

Kernel functions (kernel)¶

Template¶

template <typename Params>
struct Kernel : public BaseKernel<Params, Kernel<Params>> {
  Kernel(size_t dim = 1) {}

  double kernel(const Eigen::VectorXd& v1, const Eigen::VectorXd& v2) const
  {
      // code
  }
};

Available kernels¶

group kernel

template <typename Params>

struct Exp¶

#include <limbo/kernel/exp.hpp>

Exponential kernel (see [brochu2010tutorial] p. 9).

\[k(v_1, v_2) = \sigma^2\exp \Big(-\frac{||v_1 - v_2||^2}{2l^2}\Big)\]

Parameters:

double sigma_sq (signal variance)
double l (characteristic length scale)

Inherits from limbo::kernel::BaseKernel< Params, Exp< Params > >

template <typename Params, typename Kernel>

struct BaseKernel¶

#include <limbo/kernel/kernel.hpp>

Base struct for kernel definition. It handles the noise and its optimization (only if the kernel allows hyper-parameters optimization).

Parameters:

double noise (initial signal noise squared)
bool optimize_noise (whether we are optimizing for the noise or not)

template <typename Params>

struct MaternFiveHalves¶

#include <limbo/kernel/matern_five_halves.hpp>

Matern kernel

\[ \begin{align}\begin{aligned}d = ||v1 - v2||\\\nu = 5/2\\C(d) = \sigma^2\frac{2^{1-\nu}}{\Gamma(\nu)}\Bigg(\sqrt{2\nu}\frac{d}{l}\Bigg)^\nu K_\nu\Bigg(\sqrt{2\nu}\frac{d}{l}\Bigg),\end{aligned}\end{align} \]

Parameters:

double sigma_sq (signal variance)
double l (characteristic length scale)

Reference: [matern1960spatial] & [brochu2010tutorial] p.10 & https://en.wikipedia.org/wiki/Mat%C3%A9rn_covariance_function

Inherits from limbo::kernel::BaseKernel< Params, MaternFiveHalves< Params > >

template <typename Params>

struct MaternThreeHalves¶

#include <limbo/kernel/matern_three_halves.hpp>

Matern 3/2 kernel

\[ \begin{align}\begin{aligned}d = ||v1 - v2||\\\nu = 3/2\\C(d) = \sigma^2\frac{2^{1-\nu}}{\Gamma(\nu)}\Bigg(\sqrt{2\nu}\frac{d}{l}\Bigg)^\nu K_\nu\Bigg(\sqrt{2\nu}\frac{d}{l}\Bigg),\end{aligned}\end{align} \]

Parameters:

double sigma_sq (signal variance)

double l (characteristic length scale)

Reference: [matern1960spatial] & [brochu2010tutorial] p.10 & https://en.wikipedia.org/wiki/Mat%C3%A9rn_covariance_function

Inherits from limbo::kernel::BaseKernel< Params, MaternThreeHalves< Params > >

template <typename Params>

struct SquaredExpARD¶

#include <limbo/kernel/squared_exp_ard.hpp>

Squared exponential covariance function with automatic relevance detection (to be used with a likelihood optimizer) Computes the squared exponential covariance like this:

\[k_{SE}(v1, v2) = \sigma^2 \exp \Big(-\frac{1}{2}(v1-v2)^TM(v1-v2)\Big),\]

with \(M = \Lambda\Lambda^T + diag(l_1^{-2}, \dots, l_n^{-2})\) being the characteristic length scales and \(\alpha\) describing the variability of the latent function. The parameters \(l_1^2, \dots, l_n^2, \Lambda,\sigma^2\) are expected in this order in the parameter array. \(\Lambda\) is a \(D\times k\) matrix with \(k<D\).

Parameters:

double sigma_sq (initial signal variance)
int k (number of columns of \(\Lambda\) matrix)

Reference: [Rasmussen2006], p. 106 & [brochu2010tutorial], p. 10

Inherits from limbo::kernel::BaseKernel< Params, SquaredExpARD< Params > >

Default parameters¶

group Kernel_defaults

Functions

limbo::defaults::kernel_exp::BO_PARAM(double, sigma_sq, 1)

limbo::defaults::kernel::BO_PARAM(double, noise, 0. 01)

limbo::defaults::kernel_maternfivehalves::BO_PARAM(double, sigma_sq, 1)

limbo::defaults::kernel_maternfivehalves::BO_PARAM(double, l, 1)

limbo::defaults::kernel_maternthreehalves::BO_PARAM(double, sigma_sq, 1)

limbo::defaults::kernel_maternthreehalves::BO_PARAM(double, l, 1)

limbo::defaults::kernel_squared_exp_ard::BO_PARAM(int, k, 0)

limbo::defaults::kernel_squared_exp_ard::BO_PARAM(double, sigma_sq, 1)

Mean functions (mean)¶

Mean functions capture the prior about the function to be optimized.

Template¶

template <typename Params>
struct MeanFunction : public BaseMean<Params> {
  MeanFunction(size_t dim_out = 1) : _dim_out(dim_out) {}
  template <typename GP>
  Eigen::VectorXd operator()(const Eigen::VectorXd& v, const GP&) const
  {
      // code
  }
protected:
  size_t _dim_out;
};

Available mean functions¶

group mean

template <typename Params>

struct Constant¶

#include <limbo/mean/constant.hpp>

A constant mean (the traditionnal choice for Bayesian optimization)

Parameter:

double constant (the value of the constant)

Inherits from limbo::mean::BaseMean< Params >

template <typename Params>

struct Data¶

#include <limbo/mean/data.hpp>

Use the mean of the observation as a constant mean

Inherits from limbo::mean::BaseMean< Params >

template <typename Params>

struct BaseMean¶

#include <limbo/mean/mean.hpp>

Base struct for mean definition.

Subclassed by limbo::mean::Constant< Params >, limbo::mean::Data< Params >, limbo::mean::FunctionARD< Params, MeanFunction >, limbo::mean::NullFunction< Params >

template <typename Params>

struct NullFunction¶

#include <limbo/mean/null_function.hpp>

Constant with m=0

Inherits from limbo::mean::BaseMean< Params >

Default parameters¶

group mean_defaults

Functions

limbo::defaults::mean_constant::BO_PARAM(double, constant, 1)

Internals¶

template <typename Params, typename MeanFunction>

struct limbo::mean::FunctionARD¶

Functor used to optimize the mean function using the maximum likelihood principle

It incorporates the hyperparameters of the underlying mean function, if any

See: limbo::model::gp::KernelMeanLFOpt, limbo::model::gp::MeanLFOpt

Inherits from limbo::mean::BaseMean< Params >

Stopping criteria (stop)¶

Stopping criteria are used to stop the Bayesian optimizer algorithm.

Template¶

template <typename Params>
struct Name {
    template <typename BO, typename AggregatorFunction>
    bool operator()(const BO& bo, const AggregatorFunction&)
    {
      // return true if stop
    }
};

Available stopping criteria¶

group stop

template <typename Params>

struct MaxIterations¶

#include <limbo/stop/max_iterations.hpp>

Stop after a given number of iterations

parameter: int iterations

template <typename Params, typename Optimizer = boost::parameter::void_>

struct MaxPredictedValue¶

#include <limbo/stop/max_predicted_value.hpp>

Stop once the value for the best sample is above : ratio * (best value predicted by the model)

Parameter: double ratio

Default parameters¶

group stop_defaults

Functions

limbo::defaults::stop_maxiterations::BO_PARAM(int, iterations, 190)

limbo::defaults::stop_maxpredictedvalue::BO_PARAM(double, ratio, 0. 9)

Internals¶

template <typename BO, typename AggregatorFunction>

struct limbo::stop::ChainCriteria¶

Utility functor for boost::fusion::accumulate, e.g.:

stop::ChainCriteria<BO, AggregatorFunction> chain(bo, afun);
return boost::fusion::accumulate(_stopping_criteria, false, chain);

Where _stopping_criteria` is a ``boost::fusion::vector of classes.

Statistics (stats)¶

Statistics are used to report informations about the current state of the algorithm (e.g., the best observation for each iteration). They are typically chained in a boost::fusion::vector<>.

Template¶

template <typename Params>
struct Samples : public StatBase<Params> {
    template <typename BO, typename AggregatorFunction>
    void operator()(const BO& bo, const AggregatorFunction&)
    {
      // code
    }
};

template <typename Params>

struct limbo::stat::StatBase¶

Base class for statistics

The only method provided is protected :

template <typename BO>
void _create_log_file(const BO& bo, const std::string& name)

This method allocates an attribute _log_file (type: std::shared_ptr<std::ofstream>) if it has not been created yet, and does nothing otherwise. This method is designed so that you can safely call it in operator() while being ‘guaranteed’ that the file exists. Using this method is not mandatory for a statistics class.

Available statistics¶

group stat

template <typename Params>

struct AggregatedObservations¶

#include <limbo/stat/aggregated_observations.hpp>

TODO fallocati Write all the observations filename: aggregated_observations.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct BestAggregatedObservations¶

#include <limbo/stat/best_aggregated_observations.hpp>

TODO fallocati Write the best observation at each iteration filename: best_aggregated_observations.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct BestObservations¶

#include <limbo/stat/best_observations.hpp>

Write the best observation so far filename: best_observations.dat"

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct BestSamples¶

#include <limbo/stat/best_samples.hpp>

filename: best_samples.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct ConsoleSummary¶

#include <limbo/stat/console_summary.hpp>

write the status of the algorithm on the terminal

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GP¶

#include <limbo/stat/gp.hpp>

filename: gp_<iteration>.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GPAcquisitions¶

#include <limbo/stat/gp_acquisitions.hpp>

filename: gp_acquisitions.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GPKernelHParams¶

#include <limbo/stat/gp_kernel_hparams.hpp>

filename: gp_kernel_hparams.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GPLikelihood¶

#include <limbo/stat/gp_likelihood.hpp>

filename: gp_likelihood.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GPMeanHParams¶

#include <limbo/stat/gp_mean_hparams.hpp>

filename: gp_mean_hparams.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct GPPredictionDifferences¶

#include <limbo/stat/gp_prediction_differences.hpp>

filename: gp_prediction_differences.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct Observations¶

#include <limbo/stat/observations.hpp>

filename: observations.dat

Inherits from limbo::stat::StatBase< Params >

template <typename Params>

struct Samples¶

#include <limbo/stat/samples.hpp>

filename: samples.dat

Inherits from limbo::stat::StatBase< Params >

Default parameters¶

group stat_defaults

Parallel tools (par)¶

namespace limbo::tools::par¶

Typedefs

using limbo::tools::par::vector = typedef std::vector<X>

Functions

template <typename V>
V convert_vector(const V &v)¶

void init()¶: init TBB (if activated) for multi-core computing

template <typename F>
void loop(size_t begin, size_t end, const F &f)¶: parallel for

template <typename Iterator, typename F>
void for_each(Iterator begin, Iterator end, const F &f)¶: parallel for_each

template <typename T, typename F, typename C>
T max(const T &init, int num_steps, const F &f, const C &comp)¶: parallel max

template <typename T1, typename T2, typename T3>
void sort(T1 i1, T2 i2, T3 comp)¶: parallel sort

template <typename F>
void replicate(size_t nb, const F &f)¶: replicate a function nb times

Misc tools (tools)¶

namespace limbo::tools¶

Typedefs

using limbo::tools::rdist_double_t = typedef std::uniform_real_distribution<double>

using limbo::tools::rdist_int_t = typedef std::uniform_int_distribution<int>

using limbo::tools::rdist_gauss_t = typedef std::normal_distribution<>

using limbo::tools::rgen_double_t = typedef RandomGenerator<rdist_double_t>: Double random number generator

using limbo::tools::rgen_gauss_t = typedef RandomGenerator<rdist_gauss_t>: Double random number generator (gaussian)

using limbo::tools::rgen_int_t = typedef RandomGenerator<rdist_int_t>: integer random number generator

Functions

Eigen::VectorXd make_vector(double x)¶: make a 1-D vector from a double (useful when we need to return vectors)

template <typename T>
constexpr int signum(T x, std::false_type is_signed)¶

template <typename T>
constexpr int signum(T x, std::true_type is_signed)¶

template <typename T>
constexpr int signum(T x)¶: return -1 if x < 0; return 0 if x = 0; return 1 if x > 0.

template <typename T, typename std::enable_if< std::is_arithmetic< T >::value, int >::type = 0>
bool is_nan_or_inf(T v)¶: return true if v is nan (not a number) or infinity

template <typename T, typename std::enable_if<!std::is_arithmetic< T >::value, int >::type = 0>
bool is_nan_or_inf(const T &v)¶: return true if v is nan (not a number) or infinity (const version)

Eigen::VectorXd random_vector_bounded(int size)¶

random vector in [0, 1.0]

this function is thread safe because we use a random generator for each thread
we use a C++11 random number generator

Eigen::VectorXd random_vector_unbounded(int size)¶

random vector generated with a normal distribution centered on 0, with standard deviation of 10.0

this function is thread safe because we use a random generator for each thread
we use a C++11 random number generator

Eigen::VectorXd random_vector(int size, bool bounded = true)¶: random vector wrapper for both bounded and unbounded versions

Eigen::MatrixXd random_lhs(int dim, int n)¶: generate n random samples with Latin Hypercube Sampling (LHS) in [0, 1]^dim

std::string date()¶: easy way to get the current date

std::string hostname()¶: easy way to get the hostame

std::string getpid()¶: easy way to get the PID

template <typename D>

class RandomGenerator¶

#include <limbo/tools/random_generator.hpp>

a mt19937-based random generator (mutex-protected)

usage :

RandomGenerator<dist<double>>(0.0, 1.0);
double r = rgen.rand();

namespace par¶

Typedefs

using limbo::tools::par::vector = typedef std::vector<X>

Functions

template <typename V>
V convert_vector(const V &v)¶

void init()¶: init TBB (if activated) for multi-core computing

template <typename F>
void loop(size_t begin, size_t end, const F &f)¶: parallel for

template <typename Iterator, typename F>
void for_each(Iterator begin, Iterator end, const F &f)¶: parallel for_each

template <typename T, typename F, typename C>
T max(const T &init, int num_steps, const F &f, const C &comp)¶: parallel max

template <typename T1, typename T2, typename T3>
void sort(T1 i1, T2 i2, T3 comp)¶: parallel sort

template <typename F>
void replicate(size_t nb, const F &f)¶: replicate a function nb times